



Next: Quadratic response calculation of
Up: Directives for evaluation of
Previous: Quadratic response calculation: *QUADRA
Contents
Index
Quadratic response calculation of second order transition moments:
*QUADRA with .SINGLE RESIDUE
- .A2TEST
Test the contributions to the quadratic response function arising from
the
![$A^{\left[2\right]}$](img269.png) term. Mainly for debugging purposes.
term. Mainly for debugging purposes.
- .APROP, .BPROP
- Specify the operators
 and
and  , respectively. The line following this
option should be the label of the operator as it appears in the file
AOPROPER.
, respectively. The line following this
option should be the label of the operator as it appears in the file
AOPROPER.
- .BFREQ, .FREQUE
READ *, NFREQ
READ *, FREQ(1:NFREQ)
The frequencies 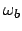 in atomic units.
Response equations are evaluated at given
frequencies. Two lines
following this option must contain 1) The number of frequencies, 2)
Frequencies.
in atomic units.
Response equations are evaluated at given
frequencies. Two lines
following this option must contain 1) The number of frequencies, 2)
Frequencies.
- .DIPLEN
Sets
 and
and  to
to 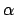 dipole operators.
dipole operators.
- .DIPLNX
Sets
 and
and  to the
to the  dipole operator.
dipole operator.
- .DIPLNY
Sets
 and
and  to the
to the  dipole operator.
dipole operator.
- .DIPLNZ
Sets
 and
and  to the
to the  dipole operator.
dipole operator.
- .E3TEST
Test the contributions to the quadratic response function arising from
the
![$E^{\left[3\right]}$](img270.png) and
and
![$S^{\left[3\right]}$](img271.png) terms. Mainly for
debugging purposes.
terms. Mainly for
debugging purposes.
- .ISPABC
READ *, ISPINA,ISPINB,ISPINC
Spin symmetry of  -operators (ISPINA),
-operators (ISPINA),  -operators (ISPINB),
and the excitation operator (ISPINC): "0" for singlet and "1" for triplet.
Default is "0,0,0", i.e. all of singlet spin symmetry.
Note: triplet operators are only implemented for singlet reference states.
-operators (ISPINB),
and the excitation operator (ISPINC): "0" for singlet and "1" for triplet.
Default is "0,0,0", i.e. all of singlet spin symmetry.
Note: triplet operators are only implemented for singlet reference states.
- .MAXITL
Maximum number of iterations for linear equations in this section.
Default is 60.
- .MAXITP
Maximum number of iterations in solving the linear
response eigenvalue
equations.
Default is 60.
- .MAXITO
Maximum number of iterations in the optimal
orbital algorithm
[22].
Default is 5.
- .MCDBTERM
Specifies the calculation of all individual components to the
 term of magnetic circular dichroism
(MCD).
This keyword sets up the calculation so that no further response input is required except .ROOTS.
The
term of magnetic circular dichroism
(MCD).
This keyword sets up the calculation so that no further response input is required except .ROOTS.
The  operator is set equal to the
operator is set equal to the  component of dipole
operator and
the
component of dipole
operator and
the  operator to the
operator to the 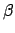 component of the angular momentum
operator. The resulting "mixed" two-photon transition moment to state
component of the angular momentum
operator. The resulting "mixed" two-photon transition moment to state 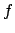 is then multiplied the dipole-allowed one-photon transition moment
from state
is then multiplied the dipole-allowed one-photon transition moment
from state 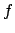 (for the
(for the  component, with
component, with
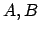 ).
[17]
).
[17]
- .MNFPHO
Specifies a phosphorescence calculation using
the atomic mean-field approximation for the spin-orbit operator, i.e.
the spin-orbit
induced singlet-triplet transition. This keyword sets up the
calculation so that no further response input is required except .ROOTS; the
 operator is set to the dipole operators and
the
operator is set to the dipole operators and
the  operator
is set to the atomic mean-field spin-orbit
operators.
The reference state must be a singlet spin state.
operator
is set to the atomic mean-field spin-orbit
operators.
The reference state must be a singlet spin state.
- .PHOSPHORESCENCE
Specifies a phosphorescence calculation, i.e.
the spin-orbit
induced singlet-triplet transition. This keyword sets up the
calculation so that no further response input is required except .ROOTS; the
 operator is set to the dipole operators and
the
operator is set to the dipole operators and
the  operator
is set to the spin-orbit
operators. [164,168]
The reference state must be a singlet spin state.
operator
is set to the spin-orbit
operators. [164,168]
The reference state must be a singlet spin state.
- .PRINT
READ *,IPRSMO
Print level. Default is 2.
- .ROOTS
READ '*',(ROOTS(I) I=1,NSYM)
Number of roots. The line following this option contains the number
of excited states per symmetry. Excitation
energies are calculated for each state and if
any operators are given,
symmetry-allowed second order transition moments are
calculated between the
reference state and the excited states.
Remember to increase .MAXRM if many frequencies are specified.
- .SINGLE RESIDUE
Required to
compute the single residue of the quadratic
response function.
For the case of dipole operators this corresponds to two-photon
transition
moments.
- .THCLR
READ *, THCLR
Threshold for solving the linear response equations.
Default is 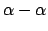 .
.
- .THCPP
READ *, THCPP
Threshold for solving the linear response
eigenvalue equation. Default is 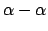 .
.
- .TWO-PHOTON
Sets up the calculation of the two-photon transition strengths. This
calculates two-photon transition strengths for all the excited states
requested by the keyword .ROOTS, calculating the necessary
quadratic response functions using the half-frequency of the
excitation energy to the given state.
- .X2TEST
Test the contributions to the quadratic response function arising from
the
![$X^{\left[2\right]}$](img278.png) term. Mainly for debugging purposes.
term. Mainly for debugging purposes.




Next: Quadratic response calculation of
Up: Directives for evaluation of
Previous: Quadratic response calculation: *QUADRA
Contents
Index
Dalton Manual - Release 1.2.1