- Integral:
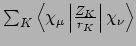
- Property label:
POTENERG
READ (LUCMD,*) DARFAC
- Integral:
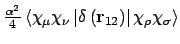
Add two-electron Darwin integrals to the standard electron-repulsion
integrals with a perturbation factor DARFAC.
- Integral:
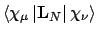
- Property labels:
XANGLON,YANGLON,ZANGLON
- Integral:
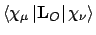
- Property labels:
XANGMOM,YANGMOM,ZANGMOM
MOLECULE.INP file (line 5).
READ (LUCMD,*) IORCAR
Cartesian multipole integrals to order
IORCAR. Read one more
line specifying order. See also the keyword
.SPHMOM.
- Integral:
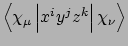
- Property labels:
CMiijjkk
IORDER, and where ii = (i/10)*10+mod(i,10).
READ (LUCMD, '(A7)') FIELD1
First derivative of the electric dipole operator
with respect to an external magnetic field
due to differentiation of the London phase
factors, see Ref. [92]. Read one more line giving
the direction of the electric field (A7). These
include X-FIELD, Y-FIELD, and Z-FIELD.
- Integral:
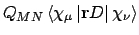
- Property labels:
D-CM1 X,D-CM1 Y,D-CM1 Z
READ (LUCMD, '(A7)') FIELD2
Second derivative electric dipole operator
with respect to an external magnetic field due
to differentiation of
the London phase factors, see Ref. [92]. Read one
more line giving the direction of the electric
field (A7). These
include X-FIELD, Y-FIELD, and Z-FIELD.
- Integral:
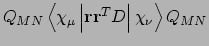
- Property labels:
D-CM2 XX,D-CM2 XY,D-CM2 XZ,D-CM2 YY,D-CM2 YZ,D-CM2 ZZ
- Integral:
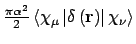
- Property label:
DARWIN
- Integral:
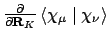
- Property labels:
1DOVLxyz
- Integral:
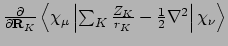
- Property labels:
1DHAMxyz
DSUSLH, DSUSLL, and DSUSNL.
- Integral:
![$\frac{1}{4}\left[\left<\chi_{\mu}\left\vert r^{2}_{N}I - {\bf r}_{N}
{\bf r}_{N...
...chi_{\mu}\left\vert{\bf r}{\bf
r}^{T}h\right\vert\chi_{\nu}\right>Q_{MN}\right]$](img137.png)
- Property label:
XXdh/dB2,XYdh/dB2,XZdh/dB2,YYdh/dB2,YZdh/dB2,ZZdh/dB2
Calculate dipole gradient integrals, that is, the geometrical first derivatives of the dipole length integrals.
- Integral:
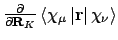
- Property labels:
abcDPG d
- Integral:

- Property labels:
XDIPLEN,YDIPLEN,ZDIPLEN
READ (LUCMD, *) (DIPORG(I), I = 1, 3)
Specify the dipole origin to be used in the calculation. Read one more line containing the three Cartesian components (*). Default is (0,0,0).
- Integral:
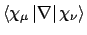
- Property label:
XDIPVEL,YDIPVEL,ZDIPVEL
- Integral:
![$\frac{3}{4}\left<\chi_{\mu}\left\vert\left[\nabla^2,\frac{{\bf r}_O^T{\bf r}_K -
{\bf r}_O{\bf r}_K^T}{r_{K}^3}\right]_+\right\vert\chi_{\nu}\right>$](img143.png)
- Property label:
abcNSKEd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the magnetic field. O is the gauge origin.
- Integral:
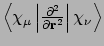
- Property labels:
dd/dxdx,dd/dxdy,dd/dxdz,dd/dydy,dd/dydz,dd/dzdz
- Integral:
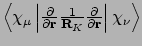
- Property labels:
DERXXPVP,DERXY+YX,DERXZ+ZX,DERYY,DERYZ+ZY,DERZZ
- Integral:
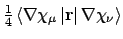
- Property labels:
PXPDIPOL,PYPDIPOL,PZPDIPOL.
- Integral:
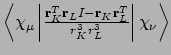
- Property labels:
DSO abcdwhereabis the symmetry coordinate of a given component for the symmetry-adapted nucleus K, andcdis in a similar fashion the symmetry coordinate for the symmetry-adapted nucleus L.
- Integral:
![$\left<\chi_{\mu}\left\vert\left[\nabla^2,\frac{{\bf r}_K^T{\bf r}_LI - {\bf r}_K{\bf r}_L^T}{r_K^3r_L^3}\right]_+\right\vert\chi_{\nu}\right>$](img148.png)
- Property labels:
DSOKabcdwhereabis the symmetry coordinate of a given component for the symmetry-adapted nucleus K, andcdis in a similar fashion the symmetry coordinate for the symmetry-adapted nucleus L.
- Integral:
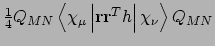
- Property labels:
XXDSUSLH,XYDSUSLH,XZDSUSLH,YYDSUSLH,YZDSUSLH,ZZDSUSLH
- Integral:
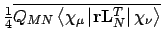
- Property labels:
XXDSUSLL,XYDSUSLL,XZDSUSLL,YYDSUSLL,YZDSUSLL,ZZDSUSLL
- Integral:
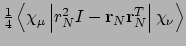
- Property labels:
XXDSUSNL,XYDSUSNL,XZDSUSNL,YYDSUSNL,YZDSUSNL,ZZDSUSNL
- Integral:
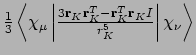
- Property labels:
xyEFGabc, wherexandyare the Cartesian directions,abcthe number of the symmetry independent center, andcthat centers c'th symmetry-generated atom.
- Integral:
- Property labels:
D1-SO XX,D1-SO XY,D1-SO XZ,D1-SO YX,D1-SO YY,D1-SO YZ,D1-SO ZX,D1-SO ZY,D1-SO ZZ
- Integral:
- Property labels:
D1-SOLXX,D1-SOLXY,D1-SOLXZ,D1-SOLYX,D1-SOLYY,D1-SOLYZ,D1-SOLZX,D1-SOLZY,D1-SOLZZ
READ (LUCMD, *) (EXPKR(I), I = 1, 3)
Cosine and sine integrals. Read one more line containing the wave numbers in the three Cartesian directions. The center of expansion is always (0,0,0).
- Integral:
- Property labels:
COS KX/K,COS KY/K,COS KZ/K,SIN KX/K,SIN KY/K,SIN KZ/K.
- Integral:
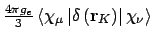
- Property labels:
FC NAMab, whereNAMis the three first letters in the name of this atom, as given in theMOLECULE.INPfile, andabis the number of the symmetry-adapted nucleus.
- Integral:
![$\frac{2\pi g_e}{3}\left<\chi_{\mu}\left\vert\left[\nabla^2,\delta\left({\bf
r}_K\right)\right]_+\right\vert\chi_{\nu}\right>$](img154.png)
- Property labels:
FCKEnacd, wherenais the two first letters in the name of this atom, as given in theMOLECULE.INPfile, andcdis the number of the symmetry-adapted nucleus.
READ (LUCMD, *) DPTFAC
A direct relativistic perturbation is added to the
Hamiltonian and metric with the perturbation parameter DPTFAC, where
the actually applied perturbation is DPTFAC*![]() .
.
READ (LUCMD, *) (GAGORG(I), I = 1, 3)
Specify the gauge origin to be used in the calculation. Read one more line containing the three Cartesian components (*). Default is (0,0,0).
- Integral:
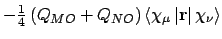
- Property labels:
HBDO X,HBDO Y,HBDO Z.
- Integral:
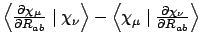
- Property label:
HDO abc, whereabcis the number of the symmetry-adapted coordinate being differentiated.
- Integral:
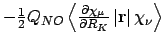
- Property labels:
abcHBD d, whereabcis the symmetry coordinate of the nuclear coordinate being differentiations, anddis the coordinate of the external magnetic field.
- Integral:
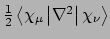
- Property label:
KINENERG.
- Integral:
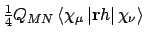
- Property labels:
XLONMOM,YLONMOM,ZLONMOM.
- Integral:
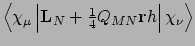
- Property label:
dh/dBX,dh/dBY,dh/dBZ.
- Integral:
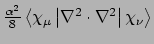
- Property label:
MASSVELO.
READ (LUCMD, *) PRTHRS
Set the threshold for which two-electron integrals should be tested
with the keyword
.MGMO2T. Default is 10![]() .
.
- Integral:
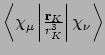 where
where 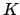 is the nucleus of interest.
is the nucleus of interest.
- Property labels:
NEF abc, whereabcis the number of the symmetry-adapted nuclear coordinate.
NSTLON and NSTNOL.
- Integral:
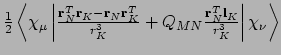 where
where 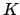 is the nucleus of interest.
is the nucleus of interest.
- Property label:
abcNST d, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the magnetic field.
- Integral:
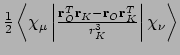 where
where 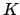 is the nucleus of interest.
is the nucleus of interest.
- Property label:
abcNSCOd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the magnetic field. O is the gauge origin.
- Integral:
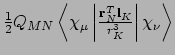 where
where 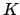 is the nucleus of interest.
is the nucleus of interest.
- Property labels:
abcNSLOd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the magnetic field.
- Integral:
 where
where 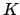 is the nucleus of interest.
is the nucleus of interest.
- Property label:
abcNSNLd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the magnetic field.
READ (LUCMD, *) INUC
Choose nuclear model. A 1 corresponds to a point nucleus (which is the default), and 2 corresponds to a Gaussian distribution model.
- Integral:
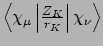 where
where 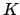 is the nucleus of interest.
is the nucleus of interest.
- Property labels:
POT.E ab, whereabare the two first letters in the name of this nucleus. Thus note that in order to distinguish between integrals, the first two letters in an atom's name must be unique.
- Integral:
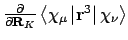
- Property labels:
abODGcde
ab is the symmetry adapted nuclear coordinate, and cde the
component (x/y/z) of the third moment tensor. Currently, this integral
does not work with symmetry.
- Integral:
![$\left<\chi_{\mu}\left\vert\left[\nabla^2,{\mathbf
l}_O\right]_+\right\vert\chi_{\nu}\right>$](img171.png)
- Property labels:
XOZKE,YOZKE,ZOZKE.
READ (LUCMD, *) (ORIGIN(I), I = 1, 3)
Set the origin appearing in the London atomic orbital phase-factors. Read one more line containing the Cartesian components of this origin (*). Default is (0,0,0).
READ (LUCMD,*) NPQUAD
Read the number of quadrature points to be used in the evaluation of the diamagnetic spin-orbit integrals, as requested by the keyword .DSO. Read one more line containing the number of quadrature points. Default is 40.
READ (LUCMD,*) IPRDEF
Set default print level during the integral evaluation. Read one more line
containing print level. Default is the value of IPRDEF
from the general input module for DALTON.
- Integral:
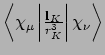 where
where 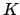 is the nucleus of interest.
is the nucleus of interest.
- Property label:
PSO abc, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate.
- Integral:
![$\left<\chi_{\mu}\left\vert\left[\nabla^2,\frac{{\bf
l}_K}{r_{K}^{3}}\right]_+\right\vert\chi_{\nu}\right>$](img173.png) where
where 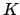 is the nucleus of interest.
is the nucleus of interest.
- Property label:
PSOKEabc, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate.
- Integral:
![$\left<\chi_{\mu}\left\vert\left[{\mathbf l}_O,\frac{{\bf
l}_K}{r_{K}^{3}}\right]_+\right\vert\chi_{\nu}\right>$](img174.png) where
where 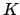 is the nucleus of interest.
is the nucleus of interest.
- Property label:
abcPSOZd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, and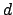 is
the direction (x/y/z) of the external magnetic field (corresponding to
the component of the orbital Zeeman operator).
is
the direction (x/y/z) of the external magnetic field (corresponding to
the component of the orbital Zeeman operator).
- Integral:
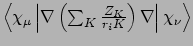
- Property labels:
pVpINTEG.
- Integral:
- Property labels:
PVIOLA X,PVIOLA Y,PVIOLA Z.
READ (LUCMD,'(A7)') FIELD3
London orbital corrections arising from the second-moment of charge operator in finite-perturbation calculations involving an external electric field gradient. Possible values for the perturbation (FIELD3) may be XX/XY/XZ/YY/YZ/ZZ-FGRD.
- Integral:
- Property labels:
ab-QDB X,ab-QDB Y,ab-QDB Z, where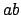 is the component of the electric field
gradient operator read in the variable FIELD3.
is the component of the electric field
gradient operator read in the variable FIELD3.
- Integral:
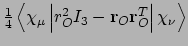
- Property label:
XXQUADRU,XYQUADRU,XZQUADRU,YYQUADRU,YZQUADRU,ZZQUADRU
Calculate quadrupole gradient integrals, that is, the geometrical first derivatives of the second moment integrals (i.e. .SECMOM, note: it is NOT the gradient of the .QUADRU integrals).
- Integral:
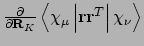
- Property labels:
abcQDGde
abc is the symmetry adapted nuclear coordinate, and de the
component (xx/xy/xz/yy/yz/zz) of the second moment tensor. Currently
symmetry can not be used with these integrals.
- Integral:
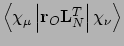
- Property label:
XXRANG,XYRANG,XZRANG,YXRANG,YYRANG,YZRANG,ZXRANG,ZYRANG,ZZRANG
READ (LUCMD,*) GAMMAC
Same as
.R12 but with Gaussian-damped linear ![]() terms of
the form
terms of
the form
![]() . The value of
. The value of ![]() is read from the input line.
is read from the input line.
- Integral:
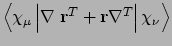
- Property labels :
XXROTSTR,XYROTSTR,XZROTSTR,YYROTSTR,YZROTSTR,ZZROTSTR.
- Integral:
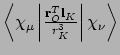 where
where 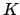 is the nucleus of interest.
is the nucleus of interest.
- Property label:
abcRPSOd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate anddrefers to the x, y, z component of the magnetic field
- Integral:
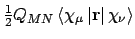
- Property labels:
dS/dBX,dS/dBY,dS/dBZ
- Integral:
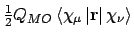
- Property label:
- Integral:
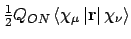
- Property labels:
- Integral:
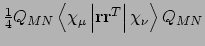
- Property labels:
dS/dB2XX,dS/dB2XY,dS/dB2XZ,dS/dB2YY,dS/dB2YZ,dS/dB2ZZ
- Integral:
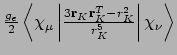
- Property label:
SD abc d, whereabcis the number of the first symmetry-adapted coordinate (corresponding to symmetry-adapted nuclear magnetic moments) anddis the x, y, or z component of the magnetic moment with respect to spin coordinates.
- Integral:
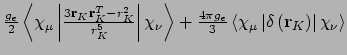
- Property label:
SDCabc d, whereabcis the number of the first symmetry-adapted coordinate (corresponding to symmetry-adapted nuclear magnetic moments) anddis the x, y, or z component of the magnetic moment with respect to spin coordinates.
- Integral:
![$\frac{g_e}{4}\left<\chi_{\mu}\left\vert\left[\nabla^2,\frac{3{\bf
r}_K{\bf r}_K^T - r_K^2}{r_{K}^5}\right]_+\right\vert\chi_{\nu}\right>$](img192.png)
- Property label:
SDKEab c, whereabis the number of the first symmetry-adapted coordinate (corresponding to symmetry-adapted nuclear magnetic moments) andcis the x, y, or z component of the magnetic moment with respect to spin coordinates.
- Integral:
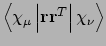
- Property labels:
XXSECMOM,XYSECMOM,XZSECMOM,YYSECMOM,YZSECMOM,ZZSECMOM
READ (LUCMD, *) NPATOM
READ (LUCMD, *) (IPATOM(I), I = 1, NPATOM
Select which atoms for which a given atomic integral is to be calculated. This applies mainly to property integrals for which there exist a set of integrals for each nucleus. Read one more line containing the number of atoms selected, and then another line containing the numbers of the atoms selected. Most useful when calculating diamagnetic spin-orbit integrals, as this is a rather time-consuming calculation. The numbering is of symmetry-independent nuclei.
- Integral:
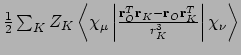
- Property labels:
SOMF XX,SOMF XY,SOMF XZ,SOMF YX,SOMF YY,SOMF YZ,SOMF ZX,SOMF ZY,SOMF ZZ.
- Integral:
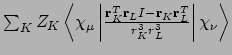
- Property label:
abcSOMMd, whereabcis the number of the symmetry-adapted nuclear magnetic moment coordinate, anddrefers to the x, y, or z component of the spin-orbit operator.
READ (LUCMD,*) IORSPH
Spherical multipole integrals to order
IORSPH. Read one more
line specifying order. See also the keyword
.CARMOM.
- Property label:
CMiijjkk
IORDER, and where ii = (i/10)*10+mod(i,10).
AO2SOINT.
- One-electron Integral:
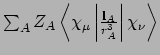 where
where 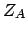 is the charge of nucleus
is the charge of nucleus  and the summation runs over
all nuclei of the molecule.
and the summation runs over
all nuclei of the molecule.
- Property labels:
X1SPNORB,Y1SPNORB,Z1SPNORB - Two-electron Integral:
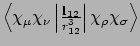
- Property labels:
X2SPNORB,Y2SPNORB,Z2SPNORB
- Integral:
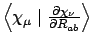
- Property label:
SQHDRabc, whereabcis the number of the symmetry-adapted coordinate being differentiated.
- Integral:
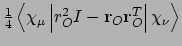
- Property labels:
XXSUSCGO,XYSUSCGO,XZSUSCGO,YYSUSCGO,YZSUSCGO,ZZSUSCGO
- Integral:
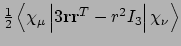
- Property labels:
XXTHETA,XYTHETA,XZTHETA,YYTHETA,YZTHETA,ZZTHETA
- Integral:
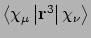
- Property labels:
XXX 3MOM,XXY 3MOM,XXZ 3MOM,XYY 3MOM,XYZ 3MOM,XZZ 3MOM,YYY 3MOM,YYZ 3MOM,YYZ 3MOM,ZZZ 3MOM.
READ (LUCMD,*) BGWEIN
Read in the square of the sin of the Weinberg angle appearing in the definition of parity-violating integrals, see .PVIOLA. The Weinberg angle factor will if this keyword is used be set to
[1-4*BGWEIN].
- Integral:
- Property labels:
ALF abcd, where is ????.
is ????.