



Next: Décomposition de l'énergie de
Up: La décompositions des interactions
Previous: La décompositions des interactions
Contents
L'interaction intermoléculaire peut se construire étape par étape par la
théorie de perturbations à symétrie adaptée (SAPT) à partir des
fonctions d'onde des monomères,
 et
et
 , solutions aux Hamiltoniens des
monomères
, solutions aux Hamiltoniens des
monomères 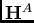 et
et  avec les énergies
avec les énergies  et
et  . La
perturbation est donnée par l'interaction électrostatique
. La
perturbation est donnée par l'interaction électrostatique 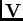 entre
les monomères et le développement de l'équation de Schrödinger en
fonction du paramètre de perturbation
entre
les monomères et le développement de l'équation de Schrödinger en
fonction du paramètre de perturbation 
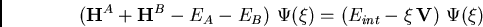 |
(20) |
permet de developper le problème en série de perturbation de
Rayleigh-Schrödinger ou ``série de polarisation''[2]Ce
développement de la méthode SAPT, mise en 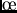 uvre dans la version 1996
de SAPT (Réf. SAPTprog) suit l'article de revue de R. Moszynsky
et al (Réf. Moszynsky).
uvre dans la version 1996
de SAPT (Réf. SAPTprog) suit l'article de revue de R. Moszynsky
et al (Réf. Moszynsky).
La méthode retenue dans la littérature pour introduire
l'antisymétrisation[3]La perturbation n'introduit pas
d'échange d'electrons entre les monomères : pour un déterminant
excité avec  et
et 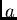 sur le monomère A,
sur le monomère A, 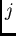 et
et 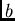 sur le monomère B
par exemple, l'élément de matrice
sur le monomère B
par exemple, l'élément de matrice
 est l'intégrale biélectronique
est l'intégrale biélectronique 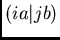 sans sa
contrepartie d'échange
sans sa
contrepartie d'échange  . correcte de
. correcte de 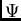 (
(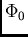 n'étant
que le produit simple de
n'étant
que le produit simple de  et
et  entre les deux monomères) est
celle nommée ``perturbation d'abord, antisymétrisation ensuite''.
L'énergie à l'ordre
entre les deux monomères) est
celle nommée ``perturbation d'abord, antisymétrisation ensuite''.
L'énergie à l'ordre  de cette série nommée ``Symmetrized
Rayleigh-Schrödiger'' s'écrit :
de cette série nommée ``Symmetrized
Rayleigh-Schrödiger'' s'écrit :
![\begin{displaymath}
E_{SRS}^{(n)}= {{1}\over{\langle\Phi_0\vert{\cal{A}}\Phi_0\...
...e\Phi_0\vert{\cal{A}}\Phi_{pol}^{(n-k)}\rangle\right] \qquad .
\end{displaymath}](img207.gif) |
(22) |
L'antisymétriseur  de l'équation 22 est représenté
en général -- afin d'obtenir des expressions maniables -- par l'échange
simple d'une paire d'électrons entre les deux monomères. La série
d'échange-répulsion de la méthode SAPT est définie comme la
différence des contributions
de l'équation 22 est représenté
en général -- afin d'obtenir des expressions maniables -- par l'échange
simple d'une paire d'électrons entre les deux monomères. La série
d'échange-répulsion de la méthode SAPT est définie comme la
différence des contributions 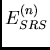 et
et 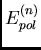 :
:
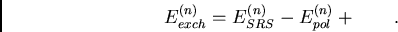 |
(23) |
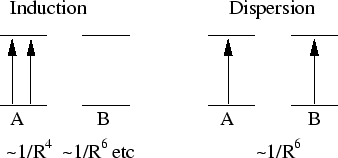
Les termes physiques de dispersion et d'induction constituent la contribution
au deuxième ordre des contributions dipolaires, schématisées sur figure
15 :
true cm
Figure 15:
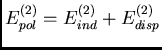 . La dispersion
a une décroissance proportionnel à 1/R
. La dispersion
a une décroissance proportionnel à 1/R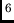 (interaction dipôle -
dipôle).
(interaction dipôle -
dipôle).
 |
En principe, les fonctions d'ondes non-perturbées des monomères devraient être
les fonctions propres exactes des hamiltoniens H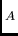 et H
et H . Or,
ces fonctions sont rarement disponibles, ce qui oblige à utiliser les
fonctions d'ondes Hartree-Fock des monomères à leur place. On ajoute
ensuite les séries de perturbation intra-moléculaires en
décomposant les hamiltoniens des monomères
. Or,
ces fonctions sont rarement disponibles, ce qui oblige à utiliser les
fonctions d'ondes Hartree-Fock des monomères à leur place. On ajoute
ensuite les séries de perturbation intra-moléculaires en
décomposant les hamiltoniens des monomères
 ,
,
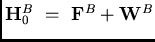 en opérateur de Fock et
perturbation. Deux contributions supplémentaires sont ainsi introduites dans les
termes de l'interaction intermoléculaire
en opérateur de Fock et
perturbation. Deux contributions supplémentaires sont ainsi introduites dans les
termes de l'interaction intermoléculaire
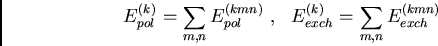 |
(24) |
où 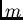 est l'ordre de perturbation en
est l'ordre de perturbation en 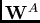 et
et  l'ordre de
perturbation en
l'ordre de
perturbation en 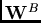 . Par la suite ces deux indices sont condensées
en
un seul par sommation partielle :
. Par la suite ces deux indices sont condensées
en
un seul par sommation partielle :
 . L'interaction électrostatique
. L'interaction électrostatique  est
améliorée significativement par d'une relaxation supplémentaire des orbitales des
monomères calculée par la théorie de la réponse (index
est
améliorée significativement par d'une relaxation supplémentaire des orbitales des
monomères calculée par la théorie de la réponse (index 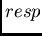 ). En revanche,
l'échange au premier ordre en
). En revanche,
l'échange au premier ordre en 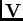 ne converge que très lentement
avec la perturbation intramoléculaire, et s'améliore par une sommation
infinie de diagrammes intramoléculaires représentant les amplitudes
Coupled-Cluster des monomères (attribut
ne converge que très lentement
avec la perturbation intramoléculaire, et s'améliore par une sommation
infinie de diagrammes intramoléculaires représentant les amplitudes
Coupled-Cluster des monomères (attribut 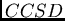 ).
).
Nous avons choisi d'utiliser la somme
en fonction de deux critères : sa disponibilité dans l'implementation de
SAPT dans les codes de Varsovie et Delaware[#!SAPTprog!#] et l'éffort du
calcul nécessaire. Nos
calculs ont démontré que cet ensemble de termes donne des résultats en
bon accord avec les calculs ab initio élaborés de type
``supermolécule''. Souvent l'énergie d'induction
 est remplacé par la contribution Hartree-Fock; on parle alors dans la
littérature de méthode ``SAPT hydride''. Malgré de meilleures performances
pour l'énergie globale d'interaction intermoléculaire nous ne
l'utilisons pas, parce que cette version mélange l'antisymétrisation au
niveau Hartree-Fock avec la perturbation intramoléculaire et une
séparation des termes d'induction et dispersion devient difficile.
est remplacé par la contribution Hartree-Fock; on parle alors dans la
littérature de méthode ``SAPT hydride''. Malgré de meilleures performances
pour l'énergie globale d'interaction intermoléculaire nous ne
l'utilisons pas, parce que cette version mélange l'antisymétrisation au
niveau Hartree-Fock avec la perturbation intramoléculaire et une
séparation des termes d'induction et dispersion devient difficile.
En conclusion de cette brève introduction à la méthode SAPT et avant
d'aborder la discussion d'alternatives moins coûteuses de décomposition en
orbitales localisées, ou leur l'équivalent dans la théorie
Heitler-London où la corrélation est incluse par la théorie des
fonctionnelles de la densité (DFT), je présente des résultats quantitatifs de
contributions obtenues par la décomposition SAPT pour trois dimères. Les
calculs ont été effectués avec une base rélativement étendue
et specifiquement adaptée aux calculs d'énergies
intermoléculaires.[#!Voisin!#]




Next: Décomposition de l'énergie de
Up: La décompositions des interactions
Previous: La décompositions des interactions
Contents
Peter Reinhardt
2004-10-05
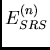 et
et ![]() et H
et H![]() . Or,
ces fonctions sont rarement disponibles, ce qui oblige à utiliser les
fonctions d'ondes Hartree-Fock des monomères à leur place. On ajoute
ensuite les séries de perturbation intra-moléculaires en
décomposant les hamiltoniens des monomères
. Or,
ces fonctions sont rarement disponibles, ce qui oblige à utiliser les
fonctions d'ondes Hartree-Fock des monomères à leur place. On ajoute
ensuite les séries de perturbation intra-moléculaires en
décomposant les hamiltoniens des monomères
![]() ,
,
![]() en opérateur de Fock et
perturbation. Deux contributions supplémentaires sont ainsi introduites dans les
termes de l'interaction intermoléculaire
en opérateur de Fock et
perturbation. Deux contributions supplémentaires sont ainsi introduites dans les
termes de l'interaction intermoléculaire
 . L'interaction électrostatique
. L'interaction électrostatique  est remplacé par la contribution Hartree-Fock; on parle alors dans la
littérature de méthode ``SAPT hydride''. Malgré de meilleures performances
pour l'énergie globale d'interaction intermoléculaire nous ne
l'utilisons pas, parce que cette version mélange l'antisymétrisation au
niveau Hartree-Fock avec la perturbation intramoléculaire et une
séparation des termes d'induction et dispersion devient difficile.
est remplacé par la contribution Hartree-Fock; on parle alors dans la
littérature de méthode ``SAPT hydride''. Malgré de meilleures performances
pour l'énergie globale d'interaction intermoléculaire nous ne
l'utilisons pas, parce que cette version mélange l'antisymétrisation au
niveau Hartree-Fock avec la perturbation intramoléculaire et une
séparation des termes d'induction et dispersion devient difficile.
