


Next: Localisation à posteriori, LPMB
Up: Le programme SCF à
Previous: Options possibles
L'option par défaut du programme ORS est le passage par l'interaction
de configuration de déterminants mono-excités pour produire des orbitales
localisées. La boucle d'itérations passe par les étapes i)
orthogonalisation,
ii) construction de la matrice Fock et calcul de l'énergie totale, iii)
construction et recherche de la valeur propre la plus basse de la matrice de
l'IC, iv) utilisation des coefficients des déterminants
mono-excités pour construire de nouvelles orbitales. A l'étape ii) nous
pouvons comparer l'élément moyen de couplage entre orbitales occupées et
virtuelles par la matrice de Fock à un seuil -- la convergence est atteinte
si cet élément disparaît en accord avec le théorème de Brillouin
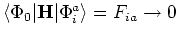 .
.
La matrice de l'IC est réduite aux contributions des éléments de la
matrice Fock, négligeant des intégrales bi-électroniques seules telles
que
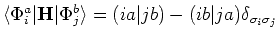 . Puisque nous faisons des calculs
à couches fermées (singulets) nous utilisons des combinaisons de spin
. Puisque nous faisons des calculs
à couches fermées (singulets) nous utilisons des combinaisons de spin
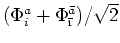 . Ceci donne
. Ceci donne
Diagonalisation de la matrice de l'IC donne des coefficients 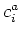 qui sont
utilisés pour mettre à jour les orbitales moléculaires :
qui sont
utilisés pour mettre à jour les orbitales moléculaires :
Cela assure que si les orbitales initiales étaient orthogonales, les espaces
des orbitales occupées et virtuelles le sont toujours :
A l'intérieur du bloc des orbitales occupées et du bloc des orbitales
virtuelles, les orbitales doivent êtres re-orthogonalisées, de
préférence par S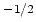 pour garder leur apparence.
pour garder leur apparence.
Les orbitales Hartree-Fock obtenues ressemblent le plus possible aux orbitales
initiales, mais nous n'avons pas de critère de maximisation ou minimisation
d'une fonctionnelle comme dans les localisation de Boys ou
Pipek-Mezey. L'avantage de cette méthode est qu'elle n'a pas besoin d'un
calcul d'orbitales canoniques avant la localisation, et nous ne délocalisons
jamais par diagonalization d'une matrice de Fock. Tout au contraire, nous
essayons de laisser localisé ce qui était localisé au début. Pour des
grands systèmes des approximation de troncature peuvent facilement être
introduites, donnant ainsi une méthode potentiellement à croissance
linèaire avec la taille du système.



Next: Localisation à posteriori, LPMB
Up: Le programme SCF à
Previous: Options possibles
Peter Reinhardt
2008-05-14
![]() . Puisque nous faisons des calculs
à couches fermées (singulets) nous utilisons des combinaisons de spin
. Puisque nous faisons des calculs
à couches fermées (singulets) nous utilisons des combinaisons de spin
![]() . Ceci donne
. Ceci donne
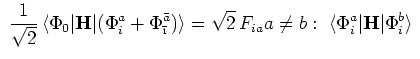
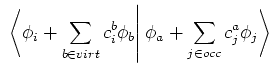
![]() pour garder leur apparence.
pour garder leur apparence.