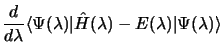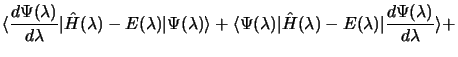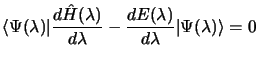suivant: Théorie des perturbations
monter: L'équation de Schrödinger et
précédent: Théorème du viriel
Théorème d'Hellmann-Feynman
Si l'hamiltonien d'un système dépend d'un paramètre 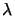 alors :
alors :
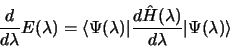 |
(3.38) |
L'équation de Schrödinger implique :
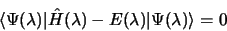 |
(3.39) |
donc
comme
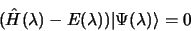 |
(3.41) |
que 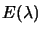 est un scalaire et en choisissant
est un scalaire et en choisissant
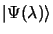 normée
normée
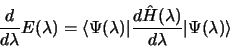 |
(3.42) |
Bernard Silvi
2005-03-16