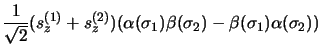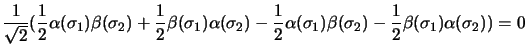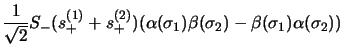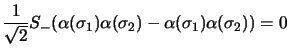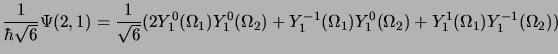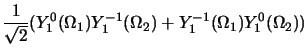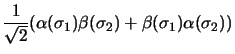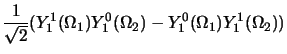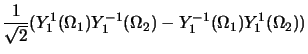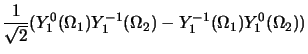suivant: Moment angulaire total
monter: Moment cinétique orbital total,
précédent: Moment cinétique orbital total,
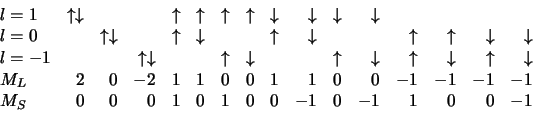
Les différentes configurations électroniques, correspondant à deux
électrons dans une sous couche 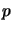 sont schématisées ci dessous
sont schématisées ci dessous
- configurations avec
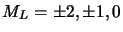 ,
, 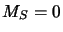 : La fonction d'espace
est de la forme
: La fonction d'espace
est de la forme
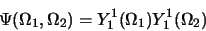 |
(2.136) |
Elle est symétrique par rapport à la permutation des électrons, et donc
la fonction de spin doit être antisymétrique, on aura
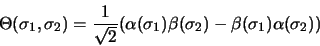 |
(2.137) |
On vérifie aisément que
et que
Cette fonction correspond bien à 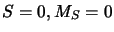 , pour obtenir
, pour obtenir
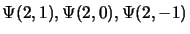 et
et 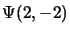 on fait agir
on fait agir 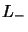 sur
sur 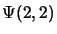
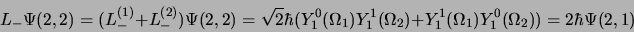 |
(2.140) |
donc
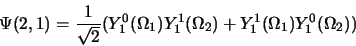 |
(2.141) |
de même
- configurations avec
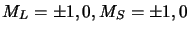 : les fonctions de spin
correspondent aux trois composantes du triplet
: les fonctions de spin
correspondent aux trois composantes du triplet
Elles sont symétriques par rapport à la permutation et par suite les
fonctions angulaires satisfaisantes doivent être antisymétriques
- configurations avec
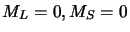 : c'est la combinaison symétrique
: c'est la combinaison symétrique
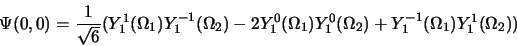 |
(2.145) |
multipliée par la fonction 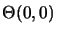 définie précédemment.
définie précédemment.



suivant: Moment angulaire total
monter: Moment cinétique orbital total,
précédent: Moment cinétique orbital total,
Bernard Silvi
2005-03-16