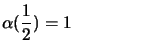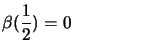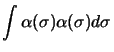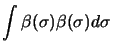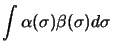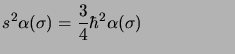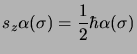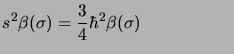suivant: Représentation matricielle de l'opérateur
monter: Le spin électronique
précédent: Le spin électronique
Dans la théorie classique du spin électronique on introduit une variable de
spin 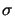 qui ne peut prendre que les valeurs discrètes
qui ne peut prendre que les valeurs discrètes
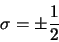 |
(2.124) |
et deux fonctions de spin
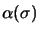 et
et 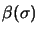 , qui forment une
base complète et ont pour valeur :
, qui forment une
base complète et ont pour valeur :
Ces fonctions sont orthonormées :
et sont fonctions propres des opérateurs 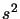 et
et 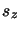



suivant: Représentation matricielle de l'opérateur
monter: Le spin électronique
précédent: Le spin électronique
Bernard Silvi
2005-03-16