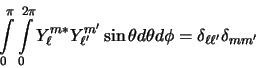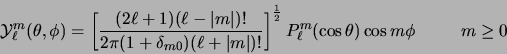suivant: Expression des harmoniques sphériques.
monter: Les fonctions propres des
précédent: Fonctions associées de Legendre.
Les harmoniques sphériques notées 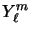 sont les solutions de
l'équation différentielle
sont les solutions de
l'équation différentielle
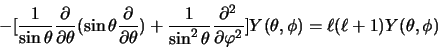 |
(2.73) |
Les variables 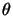 et
et 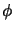 sont les coordonnées angulaires
du système de coordonnées sphériques.
sont les coordonnées angulaires
du système de coordonnées sphériques.
Cette équation est l'équation aux valeurs propres du moment
orbital.
Les solutions sont de la forme
![\begin{displaymath}
Y_\ell^m (\theta, \phi) = \left[ {(2\ell + 1)(\ell - \vert m...
...right]^{1\over 2} P_\ell^m (\cos
\theta ) \exp {\imath m\phi}
\end{displaymath}](img489.png) |
(2.74) |
Ces fonctions sont orthonormées
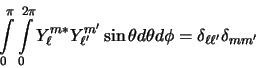 |
(2.75) |
On peut utiliser les formes réelles des harmoniques sphériques
ou harmoniques téssérales
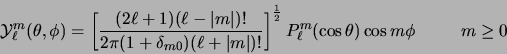 |
(2.76) |
Pour 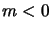
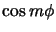 est remplacé par
est remplacé par 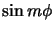 true cm
true cm
Bernard Silvi
2005-03-16
![\begin{displaymath}
Y_\ell^m (\theta, \phi) = \left[ {(2\ell + 1)(\ell - \vert m...
...right]^{1\over 2} P_\ell^m (\cos
\theta ) \exp {\imath m\phi}
\end{displaymath}](img489.png)