


suivant: Expression de l'opérateur hamiltonien
monter: Espace de Hilbert représentation
précédent: Opérateurs de projection.
Deux opérateurs 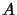 et
et 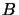 commutent si
commutent si
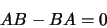 |
(1.100) |
Exemple 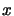 et
et 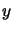
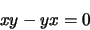 |
(1.101) |
Si 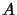 et
et 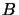 ne commutent pas il existe une règle de commutation
ne commutent pas il existe une règle de commutation
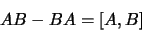 |
(1.102) |
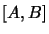 est un nouvel opérateur, le commutateur de
est un nouvel opérateur, le commutateur de 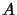 et
de
et
de 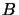 .
.
On détermine
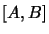 en faisant agir
en faisant agir 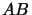 et
et 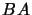 sur une fonction arbitraire
sur une fonction arbitraire 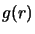
Exemple
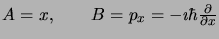
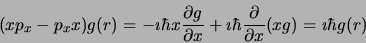 |
(1.103) |
On vérifiera facilement les relations suivantes:
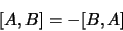 |
(1.104) |
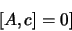 |
(1.105) |
où 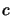 est un scalaire
est un scalaire
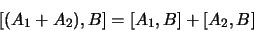 |
(1.106) |
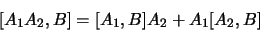 |
(1.107) |
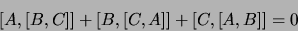 |
(1.108) |



suivant: Expression de l'opérateur hamiltonien
monter: Espace de Hilbert représentation
précédent: Opérateurs de projection.
Bernard Silvi
2005-03-16
![]() en faisant agir
en faisant agir ![]() et
et ![]() sur une fonction arbitraire
sur une fonction arbitraire ![]()
![]()